| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 |
- 정렬
- 마크다운
- 클린코드
- mysql
- 내부 정렬
- 계산 검색 방식
- @RequiredArgsConstructor
- 마크다운 테이블
- 배열
- query
- 쿼리메소드
- 스택 큐 차이
- 인터페이스
- 트리
- CleanCode
- 클래스
- @ComponentScan
- 빅 오 표기법
- 코드
- 리스트
- 선형 리스트
- @NoArgsConstructor
- WebClient
- 쿠키
- 클린
- JsonNode
- 자료구조
- 연결 리스트
- java
- code
- Today
- Total
Developer Cafe
11장 정렬 삽입 방식<삽입 정렬, 셸 정렬> 본문
정렬
순서 없이 배열되어 있는 자료들을 작은 것부터 큰 것 순서의 오름차순이나 큰 것부터 작은 것 순서의 내림차순으로 재배열하는 것이다. 정렬 방법은 수행되는 위치에 따라서 컴퓨터 메모리 내부에서 수행하는 내부 정렬과 메모리의 외부인 보조 기억 장치에서 수행하는 외부 정렬로 분류할 수 있고, 수행 방법에 따라 비교식 정렬과 분산식 정렬로 구분할 수 있다.
내부 정렬
1. 교환 방식 - 키를 비교하고 교환하여 정렬하는 방식(선택, 버블, 퀵)
2. 삽입 방식 - 키를 비교하고 삽입하여 정렬하는 방식(삽입, 셸)
3. 병합 방식- 키를 비교하고 병합하여 정렬하는 방식(2-way 병합, n-way 병합)
4. 분배 방식 - 키를 구성하는 값을 여러 개의 부분집합에 분배하여 정렬하는 방식(기수)
5. 선택 방식 - 이진 트리를 사용하여 정렬하는 방식(힙, 트리)
정렬되지 않은 { 69, 10, 30, 2, 16, 8, 31 }을 예시로 들겠다.
삽입 정렬
삽입 정렬은 정렬되어 있는 부분집합에 정렬할 새로운 원소의 순서를 찾아 삽입하는 방법이다.
1. 첫 번째 원소는 정렬되어 있는 부분집합 S로 생각하고, 나머지 원소들은 정렬되지 않은 원소들의 부분집합 U로 생각한다.
S = {69}, U = {10, 30, 2, 16, 8, 31, 22}
2. U의 첫 번째 원소 10을 S의 마지막 원소 69와 비교하여 (10 < 69)이므로 원소 10은 원소 69의 앞자리가 된다. 더 이상 비교할 S의 원소가 없으므로 찾은 위치에 원소 10을 삽입한다.
S = {10, 69}, U = {30, 2, 16, 8, 31, 22}
3. U의 첫 번째 원소 30을 S의 마지막 원소 69와 비교한다. (30 < 69)이므로 원소 69의 앞자리 원소 10과 비교한다. (30>10)이므로 원소 10과 69 사이에 삽입한다.(룰에 따라 반복)
S = {10, 30, 69}, U = {2, 16, 8, 31, 22}
4. U의 첫 번째 원소 22를 S의 마지막 원소 69와 비교한다. (22<69)이므로 그 앞자리 원소 31과 비교한다. (22<31이므로 그 앞자리 원소 30과 비교한다. (22<30)이므로 다시 그 앞자리 원소 16과 비교한다. (22>16)이므로 원소 16과 30사이에 삽입한다.
S = {2, 8, 10, 16, 22, 30, 31, 69}, U = {}
class Sort {
public void insertionSort(int a[], int size) {
int i, j, t, temp;
for(i=1; i<size; i++) {
temp = a[i];
j=i;
while((j>0) && (a[j-1]>temp)) {
a[j]=a[j-1];
j--;
}
a[j]= temp;
System.out.printf("\n삽입정렬 %d 의 단계 : ", i);
for(t=0 ; t<size; t++) {
System.out.printf("%3d ", a[t]);
}
}
System.out.println();
}
}
public class insertA {
public static void main(String[] args) {
int a[] = {69, 10, 30, 2, 16, 8, 31, 22};
int size = a.length;
Sort S = new Sort();
System.out.printf("\n정렬할 원소 : ");
for(int i=0 ; i<a.length ; i++) {
System.out.printf(" %d", a[i]);
}
System.out.println();
S.insertionSort(a, size);
}
}

셸 정렬
셸 정렬은 일정한 간격으로 떨어져있는 자료들로 구성한 부분집합 단위로 삽입 정렬을 수행하는 방법이다. 전체 원소에 대해서 정렬을 수행하는 삽입 정렬 방법에서 비교연산과 교환연산을 하는 것보다 부분집합으로 나누어 정렬하면 비교횟수와 교환연산을 줄일 수 있다.
1. 원소의 개수가 8개 이므로 매개변수 h는 4에서 시작한다. h=4이므로 간격이 4인 원소들을 같은 부분집합으로 만들면 4개의 부분집합이 만들어진다.
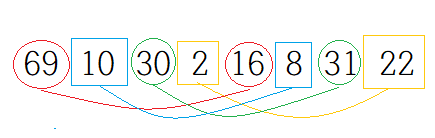
2. 첫 번째 부분집합 {69, 16}에 대해서 삽입 정렬을 수행하여 정렬한다.

3. 두 번째 부분집합 {10, 8}에 대해서 삽입 정렬을 수행하여 정렬한다.(세 번째, 네 번째도 정렬)

4. 이제 h를 2로 변경하고 다시 셸 정렬을 시작한다. h=2이므로 간격이 2인 원소들을 같은 부분집합으로 만들면 2개의 부분 집합이 만들어진다.

5. 첫 번재 부분집합 {16, 30, 69, 31}에 대해서 삽입 정렬을 수행하여 정렬한다.

6. 두 번재 부분집합 {8, 2, 10, 22}에 대해서 삽입 정렬을 수행하여 정렬한다.

7. 이제 h를 1로 변경하고 다시 셸 정렬을 시작한다. h=1이므로 간격이 1인 원소들을 같은 부분집합으로 만들면 1개의 부분집합이 만들어진다. 즉, 전체 원소에 대해서 삽입 정렬을 수행하게 된다.

class Sort5 {
public void intervalSort(int a[], int begin, int end, int interval) {
int i, j, item;
for(i=begin+interval ; i<=end ; i=i+interval) {
item = a[i];
for(j=i-interval ; j>=begin && item<a[j] ; j-=interval)
a[j+interval] = a[j];
a[j+interval] = item;
}
}
public void shellSort(int a[], int size) {
int i, j, interval, t=0;
interval = size/2;
while(interval >= 1) {
for(i=0 ; i<interval ; i++)
intervalSort(a, i, size-1, interval);
System.out.printf("\n셸정렬 %d 단계 : interval = %d >> ", ++t, interval);
for(j=0 ; j<size ; j++)
System.out.printf("%d ", a[j]);
System.out.println();
interval /= 2;
}
}
}
public class sellA {
public static void main(String[] args) {
int a[] = {69, 10, 30, 2, 16, 8, 31, 22};
int size = a.length;
Sort5 S = new Sort5();
System.out.printf("\n정렬할 원소 : ");
for(int i=0 ; i<a.length ; i++) {
System.out.printf(" %d", a[i]);
}
System.out.println();
S.shellSort(a, size);
}
}

'자료 구조 > 자바로 배우는 쉬운 자료구조' 카테고리의 다른 글
| 11장 정렬 분배 방식<기수 정렬> (0) | 2021.03.25 |
|---|---|
| 11장 정렬 병합 방식<2-way 병합, n-way 병합> (0) | 2021.03.25 |
| 11장 정렬 교환 방식<선택 정렬, 버블 정렬, 퀵 정렬> (0) | 2021.03.24 |
| 10장 트리(신장 트리, 최소 비용 신장 트리) (0) | 2021.03.21 |
| 10장 그래프 순회 (0) | 2021.03.20 |




